Efficient multivariate approximation with transformed rank-1 lattices

Robert Nasdala (Autor)

Buch | Softcover

103 Seiten

2022
Universitätsverlag Chemnitz
9783961001613 (ISBN)

Infos

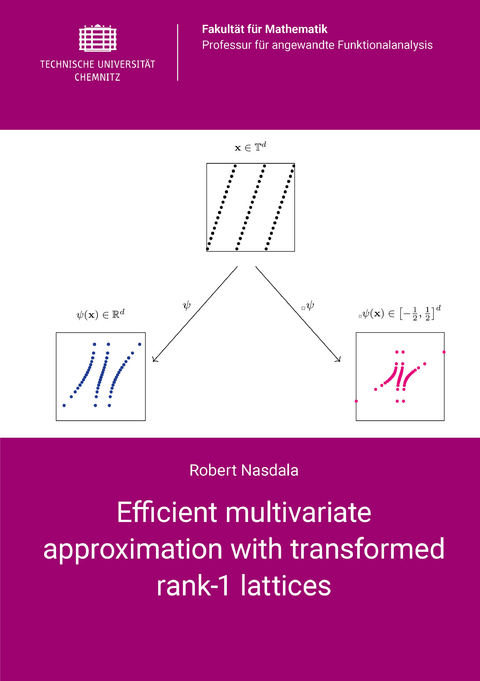
We study the approximation of functions defined on different domains by trigonometric and transformed trigonometric functions. We investigate which of the many results known from the approximation theory on the d-dimensional torus can be transfered to other domains. We define invertible parameterized transformations and prove conditions under which functions from a weighted Sobolev space can be transformed into functions defined on the torus, that still have a certain degree of Sobolev smoothness and for which we know worst-case upper error bounds. By reverting the initial change of variables we transfer the fast algorithms based on rank-1 lattices used to approximate functions on the torus efficiently over to other domains and obtain adapted FFT algorithms.

Produkt-Details

• Erscheinungsdatum: 05.01.2023
• Zusatzinfo: Diagramme
• Verlagsort: Chemnitz
• Sprache: englisch
• Maße: 148 x 210 mm
• Gewicht: 168 g
• Themenwelt: Mathematik / Informatik ► Mathematik
• Schlagworte: ank-1 lattice • Approximationstheorie • Change of variables • high-dimensional approximation Rang-1 Gitter • Hochdimensionale Approximation • Koordinatentransformation • Numerische Mathematik
• ISBN-13: 9783961001613 / 9783961001613
• Zustand: Neuware